State whether ABC and AED are congruent: a question that delves into the fascinating realm of congruence in triangles. Congruence, a fundamental concept in geometry, establishes the equality of two figures in terms of their shape and size, making it a cornerstone of geometric understanding.
This exploration will unveil the intricacies of congruence, unraveling its significance in geometry and beyond. We will delve into the methods for identifying congruent triangles, examining the relationships between their sides and angles, and uncovering the transformations that preserve congruence.
Moreover, we will discover the practical applications of congruence in various fields, showcasing its relevance in the real world.
1. Definitions and Concepts: State Whether Abc And Aed Are Congruent
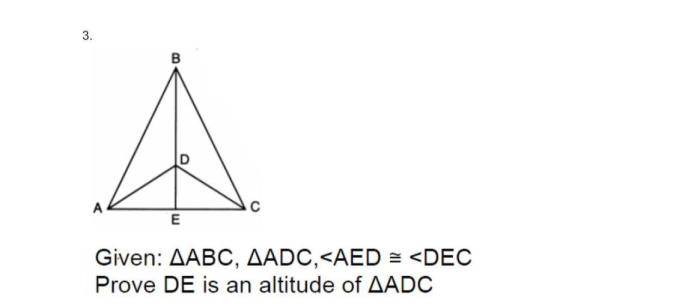
The concept of congruence plays a pivotal role in geometry, serving as a fundamental building block for understanding the properties and relationships between shapes.
Congruent triangles are defined as two triangles that have the same size and shape, meaning their corresponding sides and angles are equal in measure.
The properties of congruent triangles include:
- Corresponding sides are equal in length.
- Corresponding angles are equal in measure.
- The areas of congruent triangles are equal.
2. Identifying Congruent Triangles
There are several methods for identifying congruent triangles, each based on specific criteria that establish their equality.
The most commonly used congruence postulates are:
- SAS (Side-Angle-Side) Postulate:If two sides and the included angle of one triangle are congruent to two sides and the included angle of another triangle, then the triangles are congruent.
- ASA (Angle-Side-Angle) Postulate:If two angles and the included side of one triangle are congruent to two angles and the included side of another triangle, then the triangles are congruent.
- SSS (Side-Side-Side) Postulate:If all three sides of one triangle are congruent to all three sides of another triangle, then the triangles are congruent.
These postulates provide a solid foundation for determining congruence between triangles, enabling us to make precise deductions about their geometric properties.
3. Side and Angle Relationships
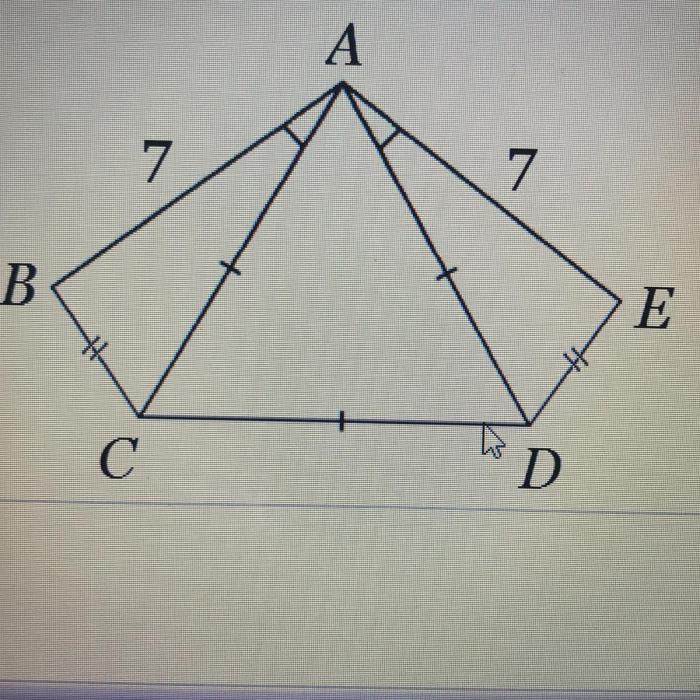
Congruent triangles exhibit specific relationships between their sides and angles, which provide valuable insights into their geometric configurations.
The following properties hold true for congruent triangles:
- If two sides of a triangle are congruent, then the angles opposite those sides are congruent.
- If two angles of a triangle are congruent, then the sides opposite those angles are congruent.
These relationships allow us to determine congruence based on specific side and angle measurements, further enhancing our understanding of triangle properties.
4. Congruence Transformations
Certain geometric transformations preserve congruence, meaning they create new shapes that are congruent to the original shape.
The three primary congruence transformations are:
- Translation:Moving a shape from one point to another without changing its size or shape.
- Rotation:Turning a shape around a fixed point without changing its size or shape.
- Reflection:Flipping a shape over a line without changing its size or shape.
These transformations provide a powerful tool for creating congruent shapes and exploring their geometric properties.
5. Applications of Congruence
The concept of congruence finds practical applications in various fields, demonstrating its versatility and significance beyond theoretical geometry.
Some key applications of congruence include:
- Architecture:Ensuring the symmetry and balance of buildings and structures.
- Engineering:Designing bridges, airplanes, and other structures that require precise measurements and congruent components.
- Design:Creating visually appealing and aesthetically pleasing designs in art, fashion, and interior design.
Congruence plays a crucial role in shaping our physical world and enhancing its aesthetic appeal.
Essential Questionnaire
What is the definition of congruent triangles?
Congruent triangles are triangles that have the same shape and size, meaning their corresponding sides and angles are equal.
How can we identify congruent triangles?
There are several methods to identify congruent triangles, including the SAS (Side-Angle-Side), ASA (Angle-Side-Angle), and SSS (Side-Side-Side) congruence postulates.
What are the practical applications of congruence?
Congruence finds applications in architecture, engineering, design, and various other fields where precise measurements and equal shapes are crucial.